
В четверг 16 марта 2023 года состоится Международная математическая конкурс-игра “Кенгуру-2023”. Олимпиаду Смарт Кенгуру по математике пишут школьники по всей России. Ниже предоставлены официальные задания и ответы для игры «Смарт-Кенгуру».
Каждый, желающий может проверить свои силы и принять участие. Сложность заданий зависит возраста участников. Различают задания для 1 и 2 класса, для 3 и 4, для 5 и 6, для 7 и 8, для 9, 10 и 11 классов. Предлагаем вашему вниманию ответы на вопросы Смарт Кенгуру 2023 для учеников 7-8 классов.
Ответы на Смарт Кенгуру 2023 для учеников 7-8 классов
1. У Смартика есть карточки с буквами его имени. Он положил их друг на друга в некотором порядке. В каком порядке лежат карточки?
Ответ: (В) СКИТАМР
2. Из листа клетчатой бумаги Смартик вырезал цифру 5 и согнул ее по стороне одной клетки. Какую картинку он может увидеть?
Ответ: (В) 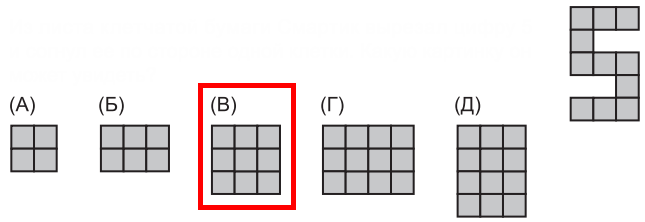
3. Чему равно -((-3)-((-2)-(-1)))?
Ответ: (Г) 2
4. Что является единицей измерения площади?
Ответ: (Г) квадратный метр
5. Два одинаковых квадратных листка бумаги наложили друг на друга так, что получилась фигура на рисунке. После этого (не смещая листы) провели два разреза. Сколько получилось частей?
Ответ: (В) 7
6. Смартик упражняется в вычислениях: он начал с числа 2023, поделил его на 1000, потом умножил на 100, потом поделил на 10. Что у него получилось?
Ответ: (В) 20,23
7. Смартик придумал шифр: круг обозначает умножение числа внутри него на 2, а квадрат — прибавление 1. На рисунке зашифровано уравнение. Чему равно х?
Ответ: (Б) 1010
8. Совсем недавно было 22 декабря 2022 года (22.12.2022). В записи этой даты шесть одинаковых цифр. В каком году встретится следующая дата с таким свойством?
Ответ: (Б) 2101
9. В ряд лежат красные и синие шарики. Оказалось, что четвёртый с конца шарик — это предпоследний красный шарик. Каким с конца может оказаться предпоследний синий шарик?
Ответ: (Б) третьим
10. Преподаватель кружка танцев обнаружил, что составить для конкурса пару мальчик-девочка можно 36 способами. Сколько детей не могло быть в кружке: 12, 13, 14, 15, 20?
Ответ: (В) 14
11. В треугольнике длины всех сторон— целые числа. Две стороны равны 20 и 23 см, а периметр треугольника делится на 5. Сколько разных значений может принимать периметр: 5, 6, 7, 8, 9?
Ответ: (Г) 8
12. У Смартика есть три карточки: две пустые, а на одной написано слово ТЫСЯЧ. Смартик написал на каждой пустой карточке слово и теперь перекладывает эти карточки в разном порядке. Иногда получается словесная запись числа. Какое наибольшее количество разных чисел могло получиться у Смартика: 1, 2, 3, 4, 5?
Ответ: (В) 3
13. На рисунке отмечены пять равных углов, два равных отрезка и угол 124 градуса. Чему равен угол, отмеченный знаком вопроса?
Ответ: (Г) 141°
14. Целые числа А, B, C таковы, что А составляет 40% от В, а В составляет 25 % от С. Чему равно частное от деления C на A?
Ответ: (Г) 10
15. Вася занимается в математическом кружке, занятия проходят2 раза в неделю. Одно занятие проходит в среду. Вася заметил, что ни в каком месяце не может быть десять занятий кружка. В какой день недели может быть второе занятие?
Ответ: (Д) суббота
16. Смартик задумал число. Ему дважды задали вопрос: «Что этоза число?» Отвечая, он каждый раз изменял задуманное число: либо уменьшал или увеличивал его на 1 или 2, либо умножал или делил его на 2 или 3. По какой паре ответов нельзя однозначно определить задуманное число: 10 и 14, 10 и 32, 12 и 20, 4 и 36, 12 и 22?
Ответ: (Д) 10, 18
17. При каком наименьшем натуральном числе k дробь 200k/20^23 является целым числом?
Ответ: (Г) 16
18. Из 32 фигурок 1*2 сложен квадрат 8*8. Смартик провёл разрез. Какое наибольшее количество фигурок могло оказаться разрезанным на две клетки?
Ответ: (Б) 8
19. На рисунке изображена прямоугольная трапеция ABCD. На ее боковой стороне отмечена точка E. Оказалось, что угол AED=60 градусов, а сумма углов BAD и EDA равна 150 градусам. AE=11, DE=7. Чему равно BC?
Ответ: (В) 9
20. В ряд стоят N человек, каждый из которых рыцарь или лжец. Рыцари всегда говорят правду, а лжец всегда лгут. Первый человек сказал:Все мы лжецы, второй сказал: Не менее половины из нас лжецы, третий сказал: Не менее трети из нас лжецы. До скольких N от 1 до 100 такая ситуация возможна?
Ответ: (В) 45


